StartDust

Hello all welcome to Stardust world.

Stardust is an application that displays data interactively asteroids that are dangerous to the earth, making a storytelling of some major asteroids, displays interactively each asteroid's orbit from the sun, together with some data from the asteroid.

the scale size of asteroids were increased to distinguish better if they would not be very small.

Design of asteroids

although each asteroid is not defined by a radius, they have elongated shapes and irregular, in the application calculate an approximate radius, why? good to accurately each asteroid had hampered the development, working with d3.js therefore to show shape and objects, use the SVG (Scalable Vector Graphics) and use [HTML_REMOVED] to plot each asteroid. This java library provides a way to read the Minor Planet Catalogues provided by the Minor Planets Center.

Data:

Semi-major axis (a): The major axis of an ellipse is its longest diameter: line segment that runs through the center and both foci, with ends at the widest points of the perimeter. The semi-major axis is one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter.

Semi-minor axis (b): The semi-minor axis is a line segment associated with most conic sections (that is, with ellipses and hyperbolas) that is at right angles with the semi-major axis and has one end at the center of the conic section.

                            b= √(1-e^2)

Eccentricity (e): The orbital eccentricity of an astronomical object is a parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptical orbit, 1 is a parabolic escape orbit, and greater than 1 is a hyperbola.

Focus (f): The distance from the center C to either focus is f = ae, which can be expressed in terms of the major and minor radii

                            f = √(a^2 - b^2)

Orbit radio (r): This value we get it follows:

                            r = a + f

Radius (radius): For the asteroids generally we use the the equatorial radius.

Period (period) : Kepler's Third Law of Planetary Motion, which correlates a asteroid's orbital period with a asteroid's distance from the Sun.

Usage

With de database they provides us and with some variables that were mentioned in the previous point, it was possible to calculate the main variables for the rotation type asteroids (ellipse), and can locate the asteroids in theirs initial position and theirs orbits

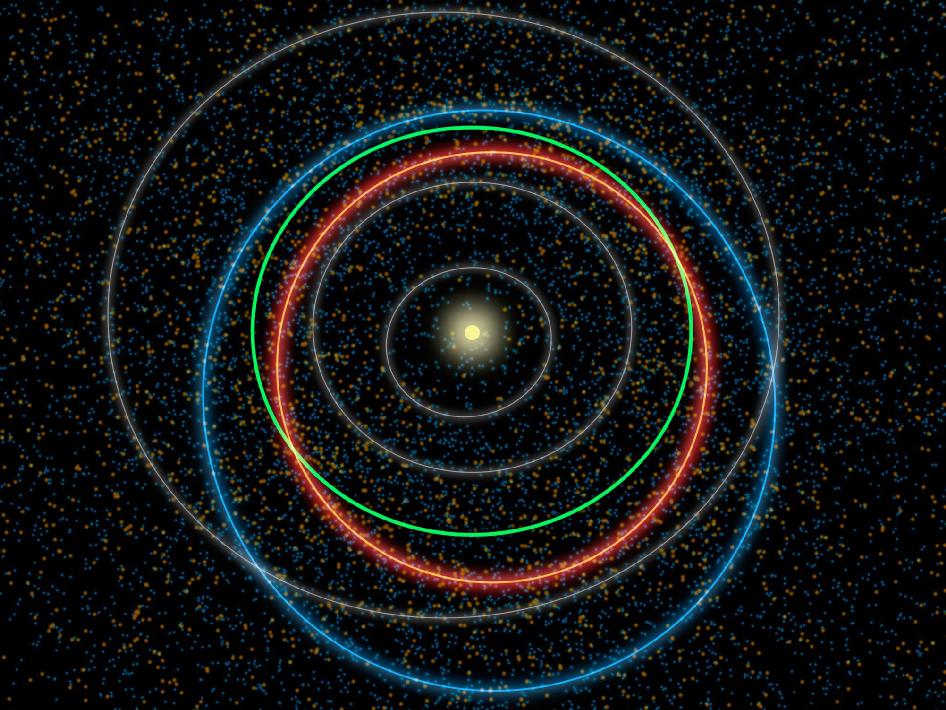
How do we calculate the orbit?

Well, first application is 2d, to calculate the orbits we use fewer variables, also imagine the orbits as ellipses also use the laws of Kepler, Kepler's laws apply to any celestial body in space.

first Klepler's law: The orbit of a planet is an ellipse with the Sun at one of the two foci.

Second Klepler's Law: A line segment joining a planet and the Sun sweeps out equal areas During equal intervals of time.

third Klepler's law: The square of the orbital period of a planet is proportional to the cube of the semi-major axis of Its orbit.

Kepler's law applies to elliptical orbits of any body in space. Newton founded the universal law of gravitation based on these laws.

Mathematically, an ellipse can be represented by the formula:

             r=p/(1+e cos(o)) (1)

where p is the semi-latus rectum, and ε is the eccentricity of the ellipse, and r is the distance from the Sun to the planet, and θ is the angle to the planet's current position from its closest approach, as seen from the Sun. So (r, θ) are polar coordinates.

For an ellipse 0 < ε < 1 ; in the limiting case ε = 0, the orbit is a circle with the sun at the centre. and we obtain that:

The semi-major axis is the equation 2:

             a =p/1-e^2 (2)

             p = a*(1-e^2) (3)

and

             r=a*(1-e^2)/(1-e*cos(o)) (1,3)

Now the function representing this formula to calculate the orbit is:

    for (var i = 0; i < resolution; i++) {
           d.theta += k / (d.r * d.r);
           d.r = d.major * (1 - d.e * d.e) / (1 - d.e * Math.cos(toRadians(d.theta)));
    }

we obtain data from an asteroid object, which has the following format:

var asteroids = [ { "major":276.75, "minor":274.36, "e":0.075823, "focus":36.29, "r":313.04, "cx":0, "cy":0, "x":276.75, "y":0, "theta": 0, "ID":2, "Radius":0.24, "period":1681.601, "speed":17.905, "name":"CERES", "discovered":2009, "class":"F", "temp":6475 }];

The data are calculated as follows:

We obtained the first data with the eccentricity "e" and Semi-major axis "major"

Run project

If you want to checkout and run the project follow these steps:

git clone https://github.com/Widrogo/StartDust.git

and open the index.html in any explorer

Project Reference

http://www.astro.washington.edu/users/smith/Astro150/Tutorials/Kepler/

http://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion

https://www.khanacademy.org/computer-programming/elliptic-orbit-with-the-correct-speed/1979432907

Bluemix link

stardust.mybluemix.net

Project Information

Resources